Math, Science and Consciousness

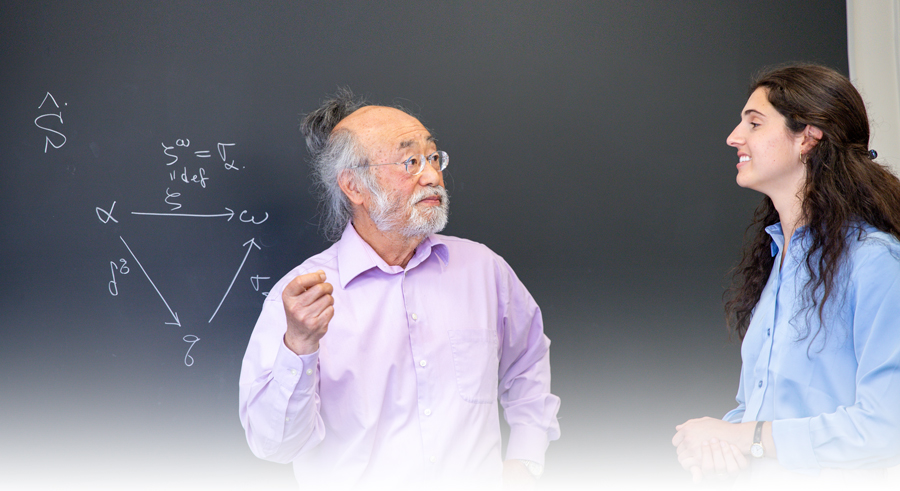Q&A

A CONVERSATION ABOUT PURE MATH, TEMPORAL TOPOS, DEEP THINKING AND THEIR UNIFYING BEAUTY

OCTOBER 2025
Q&A FACILITATED BY EILEEN ODANAKA VAVRA  / PHOTOS BY ALEXIS KOVACEVIC

---

Eileen Vavra: Learn by Doing is the key principle at Cal Poly. Was this prominent in your teaching style?

Goro Kato: The Cal Poly motto is probably saying don't be so far away from the reality going on in society that you end up learning only the theory of how something should work without checking if it really works or not. Learning by doing is important, but I have to say, learning by profound thinking is very important. Deep thinking and tremendous concentration are almost a necessity for mathematics because the higher you go, it gets more difficult to understand. So you cannot do halfway. You have to take a huge bite and chew it. Learn by deep thinking, many hours of thinking.

EV: That could be a good motto, as well. Tell us more about how you practice learning by deep thinking.

GK: When I was a graduate student, my advisor was Professor Saul Lubkin. He got his Ph.D. from Harvard when he was 22 years old. But that’s the least impressive of his achievements. He proved Weil conjectures when he was 24 and was invited to speak everywhere. When I was learning from him, I was shocked at how deep he was in mathematics and how beautiful it was. I knew I had better almost risk my life to understand what this man was talking about. It was necessary for me to have a huge concentration and very deep thinking and continue to think almost all the time, even in dreams. So that's what I mean by deep thinking.

EV: While thinking about and studying mathematics, what have you found that was beautiful?

GK: To be explicit about what the beauty is, I have to explain mathematics. In my area of study, p-adic cohomology theory and zeta invariants, you have to master many theories to really understand it. In some moments, you can see all those different theories united as one theory, and that is beautiful to me to see how they fit together.

I try to present this view through my Math 580 seminar here at Cal Poly with graduate students and faculty members. I love to share what I think is incredible and beautiful. In October, I gave a series of talks in Germany about this and my new book. And again, there's a beautifully unified view about quantum physics, relativity, as well as life sciences-involved biology. Biological science is extremely complex, and in a way, more complex than theoretical physics. Historical philosophers were aware of this reality, but they didn't know the mathematical language to express it. Mathematics is so powerful, and I try to mathematically express the realm of reality in my book.

(Frost Research Scholar and fourth-year mathematics student Elli Sumera joins the conversation by Zoom.)

Elli Sumera: Hi Dr. Kato, how are you doing? I think your book does a great job of introducing the basics of category theory. Do you feel that category theory should be integrated into undergraduate mathematics curricula and where do you see category theory fitting into the larger scope of math research as a unifying branch of mathematics?

GK: You’re right, it’s a very unifying theory. In the U.S., category theory is usually introduced — at the earliest — at the master’s level. My opinion is category theory should be introduced even earlier to undergraduates. It's a very modern theory, meaning post-Bourbaki. The Bourbaki group basically gave us new language for modern mathematics, but you can build the mathematics based on category theory. Having said that, Elli, you have to be very careful with category theory. It has its own charm. If you become category theorist, it may be difficult to find a job. Other pure mathematicians may not be able to appreciate your categorical language. But it is a useful tool.

EV: This sounds intriguging. For us non-mathematicians, could one of you briefly describe what category theory is? I have no idea!

ES: I haven't formally studied category theory, but this is how I would introduce it. In the different branches of mathematics, we generally have sets, and functions that relate those sets. For example, in linear algebra, we study vector spaces and linear transformations. In abstract algebra, we study groups and group homomorphisms. Category theory is a generalization of these ideas, where any mathematical concept is called an object and the relations between objects are called morphisms. So, category theory provides us with a language that applies to most areas of mathematics. Do you want to add to that, Dr. Kato?

GK: You said it beautifully, Elli! That’s exactly it. Accurate!

ES: For me as an undergraduate and aspiring mathematician, category theory helps with baseline knowledge. I think it has an important future in what math education — and especially research — will look like. Which leads to my next question, Dr. Kato. First, it's incredible that you've spent so much of your life developing this theory, and you explain it as a unified mathematical foundation of natural philosophies. How do you hope that your theory will impact research in the natural sciences and in philosophy? And how do you think researchers can use your theory to unify their work amongst the other fields?

GK: With philosophy, if you listen to the terminologies used by historical Eastern and Western philosophers, there is something in common. They were very bright people and looking in the same direction, like various angles. This, I try to unify with my theory in Temporal Topos. Some philosophers were talking about something similar, but not quite the same. Mathematically, we have an isomorphism, meaning it's essentially the same, but doesn't have to be equal. This can be very handy when trying to unify the various thoughts. With the sciences, a serious one is theoretical physics. It’s almost dangerous to talk about measurement. Elli, do you know measurement problem?

ES: Yes, I was just reading about it in your book.

GK: Ok, great European philosophers and some physical physicists have had to pull out the notion of divine existence. In general, scientists don't like that. In the temporal topos, the initial object in a category plays a role. Nothing divine or holy about it, just an initial object that satisfies certain conditions. That fits so well with the theory, thanks to mathematics.

I owe so much to mathematics. Mathematics speaks, and I must listen what mathematics says. Temporal topos is an ur-functor category having an initial object and a terminal object. That means these are constant ur-functors, i.e., nothing to do with objects of temporal site S. Consequently, the ‘Omni’ concept — as in omnipresent, omnipotent, omniscient — comes from the constant-ness of these ur-functors as an initial object and a terminal object.  Philosophers’ notions like Kant’s ‘Ding-an-Sich’, Leibniz’s the source of monads, Hegel’s the Whole of Spirit, Brahman in Hinduism, the Way in Taoism, Plato’s Forms, etc., are characterized as an initial object of a temporal topos.

ES: You're using pure mathematics to talk about interdisciplinary ideas. Do you think researchers in other fields, like natural sciences, would benefit from having a background in some pure mathematics?

GK: Indeed, confidently, yes. But practically, you know how hard it is for most people to understand mathematics. As people become more specialized, communicating the work gets harder. Take life sciences, for example. We have a body, and at the same time, we are thinking. This is the reality. Temporal topos explains this reality. We think using the brain cells and atoms. And we think and communicate using the mental world. Temporal topos gives you the framework for how we communicate. So, suddenly it becomes crucial to know category theory, sheaf theory, topos and pure mathematics  with this type of work. I have been so careful to make sure my theory is mature so that there are no contradictions. That's the severity of mathematics. Contradiction is not allowed.

Elli, I'd like to pose to you the same question you asked.

ES: I do believe pure mathematics is something that anyone could benefit from. I just finished three years of my undergraduate mathematics degree, and already the study of pure mathematics is making me a better thinker and problem solver and helping me with critical thinking.

It's so beautiful, and I feel it reflects a lot of the natural ways that we think about the world around us, or like what Dr. Kato is talking about, of reality. I do think it's unifying subject that can be found in any field.

I have one more question for you, Dr. Kato. For the development of your theory, you mentioned that it has applications to quantum mechanics and biological sciences. How much did you collaborate with experts in those fields to see how your theory would apply? And how did they react to your theory and your pure mathematical approach?

GK: I have learned from various books and people, but communication of the theory with others is a difficult one. I'm sure, Elli, you already know that if you try to talk about mathematics with someone who doesn’t study mathematics, it's not so easy, is it?

ES: No, it’s not.

GK: I think you know how difficult it is because for math majors, the work is so rigorous and there are no loose ends. Most people are not mentally trained for that.

EV: I bet if anyone can do it, it’ll be Elli.

GK: Yes, you can be the significant bridge between pure mathematics and other areas. You are so aware, even at your young age.

ES: Having more interdisciplinary activity between mathematicians and other fields would be helpful. Even in our own college, for summer undergraduate research, the math majors sort of stay in their own group, whereas the other fields collaborate more between chemistry and biology and other areas. I think it is what you're saying. Dr. Kato, that it does require a lot of background knowledge to even understand much of what the mathematicians or math students are talking about. So it's definitely something to think about — how can we make it more accessible to the other fields in the sciences.

GK: Yes, the division of special fields started from the 20th century. Within mathematics, I think Hilbert was the last person who knew many fields, and after that, it's very difficult to find a great mathematician who has a broad, deep understanding of many fields. It’s very challenging to understand different fields.

ES: I think so, it is very challenging. Well, that is all I prepared. Thank you so much, Dr. Kato, for answering my questions.

GK: Your questions were very sharp, Elli! 

EV: And I thank you both, as well. That was an excellent and intriguing Q&A.
 

Kato with Dean Wendt, dean of the Bailey College of Science and Mathematics. "Goro could remember each student's name for every class he taught," said Wendt, who had been in Kato's class as an undergraduate.